Die Hearings des Start-Preises fanden in der Österreichischen Nationalbank statt – nach langerer Wartezeit, die sich die Nominierten mit einem Spaziergang durch die umfangreiche Ausstellung vertreiben konnten, dauerte das Hearing selbst nur wenige Minuten. Ein Anruf aus dem FWF-Prasidium informierte mich dann bald, dass mein Projekt genehmigt wurde. Ich war erleichtert – nur rund zehn Prozent der Nominierten erhalten auch einen Preis.
Das Projekt spaltet sich auf recht naturliche Weise in zwei Teile: Ein Teil ist eher grundlagenorientiert und fokussiert auf Fragen aus Analysis und Zahlentheorie. Der zweite Teil ist anwendungsnäher und beschäftigt sich mit Fragen aus der numerischen Mathematik und Computermathematik.
Grundlagen
Eines der Themen meiner Forschungsarbeit ist die metrische Zahlentheorie – eine Theorie, die sich mit „typischen“ Eigenschaften reeller Zahlen beschaftigt. Dazu sollte man sagen, dass es in der Mathematik verschiedene Größenordnungen von unendlich gibt, namlich „abzählbar unendlich“ und „uberabzählbar unendlich“. Abzählbar unendlich sind Mengen, die man auf einer unendlichen Liste aufschreiben konnte, immer ein Element nach dem anderen – von dieser Größenordnung sind etwa die ganzen Zahlen oder (etwas überraschend) die Menge der rationalen Zahlen, also der Bruchzahlen. Die reellen Zahlen hingegen (also alle Zahlen, die sich in unendlicher Dezimalentwicklung schreiben lassen) sind überabzählbar – man könnte sie also auch auf einer unendlichen Liste nicht eine nach der anderen aufschreiben. Das alles ist vielleicht etwas irritierend, wenn man es das erste Mal hört, und es ist nicht überraschend, dass Georg Cantor, der Entwickler dieser (heute allgemein anerkannten) Theorie der Unendlichkeiten zunächst heftig angefeindet wurde.
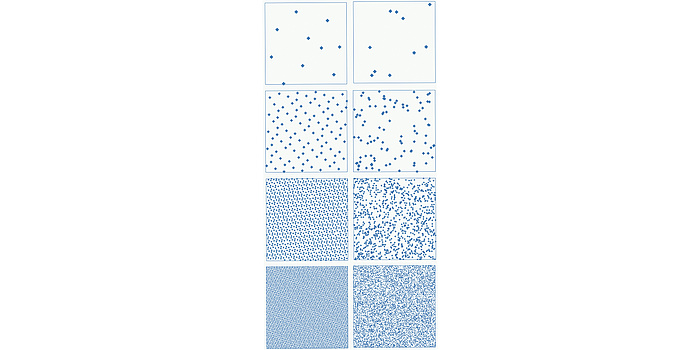
Zufällige Punkte (rechte Spalte) und spezielle, sehr gleichmäßig verteilte Punkte (sogenannte Niedrigdiskrepanz-Punkte, linke Spalte). In der obersten Zeile 10, dann 100, 1.000 und schließlich 10.000 Punkte. Die Punkte rechts entsprechen der Monte-Carlo-Methode, die Punkte links der Quasi-Monte-Carlo-Methode. Die Niedrigdiskrepanz-Punkte füllen das Quadrat regelmäßiger als die zufälligen Punkte – sie sind zur numerischen Integration daher besser geeignet.
Um zur metrischen Zahlentheorie zurückzukommen: Da es also sehr viele reelle Zahlen gibt, kann man nicht versuchen, sie eine nach der anderen zu untersuchen. Stattdessen ist es naheliegend, Eigenschaften zu finden, die (in einem sehr genauen Sinn) fur alle „typischen“ reellen Zahlen gelten. So taucht etwa bei einer typischen reellen Zahl die Ziffer 0 nach dem Dezimalpunkt (asymptotisch) gleich oft auf wie die Ziffer 1. Wenn der Leserin oder dem Leser all das unbegreiflich ist, dann wird sie oder er zumindest glauben, dass es sich bei diesem Teil um den eher theoretischen Teil des Projekts handelt – von Anwendungen in der sogenannten wirklichen Welt ist all das tatsächlich recht weit weg. Für die Mathematikerin bzw. den Mathematiker ist das freilich kein Hinderungsgrund – ganz im Gegenteil, wenn, wie auf diesem Gebiet, verschiedene mathematische Disziplinen ineinandergreifen (zum Beispiel Zahlentheorie, Fourier-Analysis, Wahrscheinlichkeitstheorie, Ergodentheorie) und sich nach und nach die Zusammenhange zwischen verschiedenen Phänomenen offenbaren, dann ist das ein wunderbarer intellektueller Genuss.
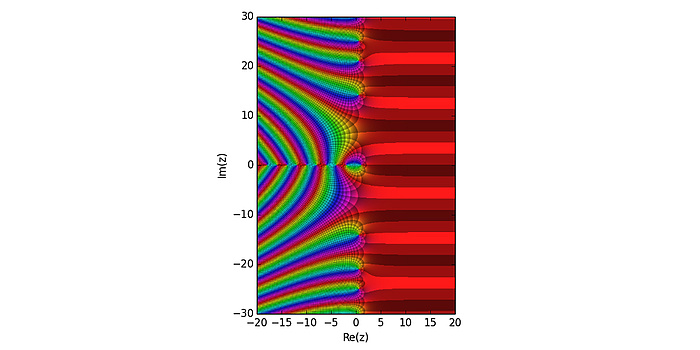
Die Riemannsche zeta-Funktion „verschlüsselt“ viele Eigenschaften von zahlentheoretischem Interesse, etwa die Anzahl an Primzahlen bis zu einer gewissen Größenordnung. Die Funktion ändert zwischen Realteil 0 und 1 (untere Achse) ihr Verhalten – die Erforschung der zeta-Funktion in diesem „kritischen Bereich“ gehört zu den Themen dieses Projekts, und zu den wichtigsten mathematischen Problemen überhaupt.
Praxis
Stellen Sie sich vor, Sie wollen ein Integral berechnen, und zwar die durchschnittliche Tiefe eines Gewässers. Eine exakte Lösung zu bekommen, ist unmöglich, daher verwenden Sie eine Näherungsmethode. Eine Möglichkeit wäre die sogenannte Monte-Carlo-Methode: Sie wählen eine große Zahl von zufälligen Punkten auf der Seeoberfläche und bestimmen dort die Tiefe des Sees – die tatsächliche durchschnittliche Seetiefe wird dann ungefähr so groß sein wie der Durchschnittswert an diesen zufälligen Punkten. Der Fehler allerdings wird von der zufälligen Auswahl der Messpunkte abhängen – wobei auch nicht ganz klar ist, wie man „zufällige“ Punkte überhaupt auswählt. Die sogenannte Quasi-Monte-Carlo-Methode folgt einem anderem Prinzip – statt rein zufälliger Punkte verwenden Sie sorgfältig ausgewählte (nichtzufällige) Messpunkte. Man kann zeigen, dass diese Methode oft ein deutlich besseres Ergebnis liefert. Und jetzt stellen Sie sich vor, Sie wollen nicht ein zweidimensionales Integral (wie im Beispiel der durchschnittlichen Seetiefe) berechnen, sondern ein tausenddimensionales. Das klingt fur den Laien vielleicht absurd (schließlich ist die „normale“ Welt nur dreidimensional), ist aber für Anwendungen extrem wichtig – wenn Sie beispielsweise den erwarteten Schaden bei der Versicherung mit 1.000 Versicherungsnehmerinnen und –nehmern berechnen wollen, dann ist das eben ein 1.000-dimensionales Integral. Wieder kann die Quasi-Monte-Carlo-Methode gute Ergebnisse liefern – aber viele Fragen sind für solche Probleme noch offen, und zwar ganz praktische Probleme von der Sorte: Bis zu welcher Größenordnung kann ich das Ergebnis effizient am Computer berechnen lassen? Wie wirkt sich eine Erhöhung der Dimension aus? Kann ich nur einfache oder auch komplizierte Funktionen integrieren?
Christoph Aistleitner (links) mit seinem Sohn Paul und dem (damaligen) Staatssekretär Harald Mahrer bei der Verleihung des FWF-Start-Preises 2015 in Wien.
So weit eine kurze Beschreibung der Themen, die dem Projekt zugrunde liegen. Die tatsächlichen Forschungsfragen sind natürlich deutlich spezialisierter und deutlich komplexer. Gemeinsam mit mir arbeiten zwei Postdoc-Wissenschafter und ein Doktoratsstudent in diesem Projekt. Alle drei Stellen wurden international ausgeschrieben, und für alle drei Ausschreibungen gab es eine sehr große Zahl an (qualifizierten) Bewerbungen – für mich eine deutliche Bestätigung der Attraktivitat der TU Graz fur junge internationale Wissenschafterinnen und Wissenschafter.
Dieses Forschungsgebiet ist im FoE „Information, Communication & Computing“ verankert, einem der fünf Stärkefelder der TU Graz.
