Computational Fluid Dynamics - Solvers
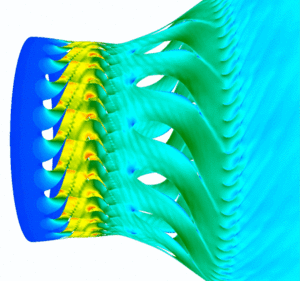
The institute has developed its own flow solver named LINARS in 2005 which was continuously improved and enlarged since then. In 2011 a block-based parallelisation was implemented based on OpenMP. In 2014 an MPI parallelization allows to use CPUs on different nodes.
LINARS is written in the object orientated programming language C++. It is therefore easy to maintain and extend. Inheritance and polymorphism is applied to access turbulence models. Class structure allows easy implementation of new turbulence models or boundary conditions.
The main features of the code are:
- Time-iterative solution of the compressible Reynolds/Favre averaged Navier-Stokes (RANS) equations
- Fully implicit time integration based on Newton-Raphson procedure
- Finite volume discretization on structured curvilinear grids in multiblock alignment
- Inviscid (Euler) fluxes are discretized with the upwind flux-difference splitting method of Roe
- Third-order MUSCL interpolation to get the state vector at each cell interface for high order of spatial accuracy
- A total variation diminishing (TVD) scheme is used to improve shock resolution
- Viscid flux vector discretization with a second-order accurate central-differencing scheme using Green’s theorem
- Implicit solution of the resulting equation systems with a line Gauss-Seidel method
- The main flow equations and the turbulence equations are solved sequentially
- Non-reflecting boundary conditions based on Giles
- Phase-lagged boundary conditions for unsteady simulations in order to reduce the flow domain
- Pressure-gradient sensitive wall function
-
Turbulence and transition models
- Spalart-Allmaras one-equation model
- Wilcox k-omega model
- Menter’s SST model
- Laminar kinetic energy model by Leylek and Walters
- V2-f and zeta-f non-linear eddy viscosity model
- Menter’s gamma-Re_theta two-equation transition model
- LES
Additionally, commercial codes such as ANSYS CFX/FLUENT are used.