Theoretical Physics for Cardiovascular Surgery
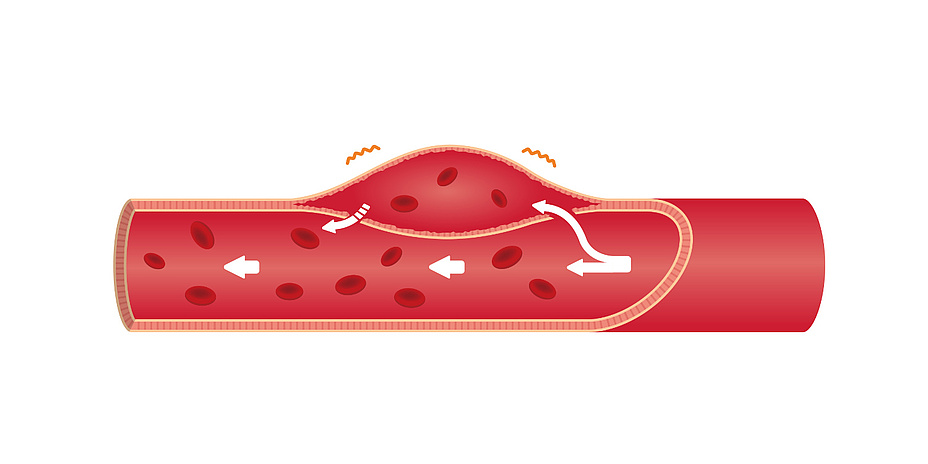
Ms Z (56) is admitted to hospital with severe chest pains, shortness of breath and a frightening feeling of impending doom. What initially looks like a heart attack actually has a completely different cause: a type B aortic dissection (detachment of the wall layers of the aorta), which means that the descending aorta is affected. The aorta is the largest artery in the human body. It channels the blood directly from the left ventricle into the bloodstream. If something is not right here, the highest alarm level rules. Ms Z’s life is possibly in acute danger.
I, Sascha Ranftl (31), physicist, would like to help Ms Z. As part of an interdisciplinary team in the LEAD-Project “Mechanics, Modeling and Simulation of Aortic Dissection” at Graz University of Technology (TU Graz), I work on computer simulations of the aorta and numerical algorithms for the risk assessment of aortic dissections. Our goal: technical assistance for medicine.
Haematoma in the vessel wall
In simple terms, an aortic dissection is a haematoma in the vessel wall of the aorta. This haematoma results from a tissue defect in the vessel wall, which is a few millimetres thick. Comparable to a lasagna, it consists of many thin, overlapping layers of cells. Starting from small tears in the inner cell layers of the inner side of the vessel wall (tunica intima), the blood from the artery presses into the tears and penetrates further into the wall (tunica media). The pressure and force exerted by the blood flow cause the cell layers to separate from each other and the “lasagna sheets” to peel off. The resulting cavity, a so-called false lumen, fills with blood and continues to expand. The false lumen can be several centimetres thick and up to 30 centimetres long.
An acute aortic dissection can lead to organ failure if, for example, it blocks the blood supply to the kidneys. In the worst case, the aorta can tear – a so-called aortic rupture. Both require immediate emergency open-heart surgery. Depending on the severity, up to 40% of cases are fatal. A chronic or “stable” aortic dissection, on the other hand, does not show such dramatic complications.
Still a difficult decision
Even with state-of-the-art computerised tomography, it is by no means clear whether a stable aortic dissection will remain stable, or whether or when it will become acute. Doctors are faced with a difficult problem that can make the difference between life or death. Can Ms Z be stabilised with blood-pressure lowering medication and continue to live (almost) without restrictions and complaints for many years? Or is complex and risky open-heart surgery necessary to replace the aorta with an artificial tube? According to the current state of the art, medical professionals rely mainly on their intuition and experience when making this decision. So, does Ms Z’s doctor have a good intuition for this? Both would want to see a more objective decision-making process.
My research focuses on the quantitative assessment of the uncertainties and risks associated with aortic dissections. I use computer simulations of fluid dynamics and biomechanics that describe the blood flow and mechanical forces in the vessels. I also need machine learning and probability theory methods to make quick predictions. Although the simulations allow for reliable and accurate forecasts, they require several weeks of computing time on a supercomputer. By then, however, it may already be too late for Ms Z.
This “computation time problem” is exacerbated by another aspect. For meaningful statistics, we need several tens to hundreds of thousands of simulations, each of which requires weeks of computation time. Some physico-physiological parameters cannot be measured precisely “in vivo”, i.e. in a living patient. For example, the flow properties of the blood or the tissue stiffness of the aorta of a living person are difficult to determine.
A trick saves centuries
We therefore have to carry out our calculations without knowing the exact properties of the tissue. Our only option is to simulate all physically plausible values of these parameters. Depending on the number of unknown parameters, this involves many thousands of combinations of parameter values, and the calculation time can take centuries.
A trick is needed to achieve a result despite the computation time problem. In my doctoral thesis, I developed an artificial intelligence (so-called Gauss process) that extracts and learns the quintessence of the simulated fluid dynamics and biomechanics from a handful of example simulations. The learning process is quite complex, but afterwards the artificial intelligence can predict new simulations for unknown parameter values approximately – and in fractions of a second instead of weeks or months. Computation time problem solved.
This allows the mechanical forces driving the aortic dissection to be estimated and understood at the time of diagnosis, when it is medically urgent and critical, rather than weeks later.
The bridge between simulation and reality
And how can the risk be calculated from a multitude of simulations? Luckily, theoretical physicists have developed the theory of probability over the past century. Using probability theory, I was able to collate all this physico-physiological information and data and calculate a quantitative estimate of risk and uncertainty. This is how we bridge the gap between computer simulation and reality.
Using a large number of simulations, I calculated a mean value and a fluctuation range – i.e. an uncertainty – for the mechanical stress. A tissue ruptures as soon as this mechanical stress exceeds a critical limit value. In addition, the probability that the mechanical stress will “fluctuate above” this critical limit value can also be calculated. The more the mechanical pressure fluctuates, the more likely it is that the limit value will be exceeded.
Analysis merely a basis for decision-making
Let me give an example. The mechanical stress caused by the systolic flow pressure in the aorta alone is typically a few tenths of a millibar (mbar). An average mechanical stress with a fluctuation range would be 0.7 mbar plus/minus 0.01 mbar. In this case, the probability that the mechanical stress will be greater than a limit value of 0.8 mbar is very low. However, if we had a larger fluctuation range of 0.7 plus/minus 0.2 mbar – with the same mean value – the risk of exceeding the limit of 0.8 mbar would be much greater. The medical significance of a probability of 0.1% for the limit value to be imminently exceeded leading to an aortic rupture WITHOUT surgical intervention would be quite different if this figure were to be 10% or even 50%. And the indicated choice of therapy would be completely different in each case.
Ms Z has been lucky. Her risk is 0.1%, so the mechanical stress fluctuates within acceptable limits. She is spared the operation. At least, for the time being.
However, neither theoretical physics nor cardiovascular surgery can say where the personal limit for acceptable risk lies. Ultimately, these decisions are in the hands of the patients and doctors, but with the simulations and the uncertainty analysis they have a quantitative, technical basis for decision-making.
This research area is anchored in the Field of Expertise “Human & Biotechnology”, one of five strategic foci of TU Graz.
You can find more research news on Planet research. Monthly updates from the world of science at Graz University of Technology are available via the research newsletter TU Graz research monthly.
Kontakt
Sascha RANFTL
Dipl.-Ing. Dr.techn. BSc
TU Graz | Institute of Theoretical and Computational Physics
ranftl@tugraz.at




