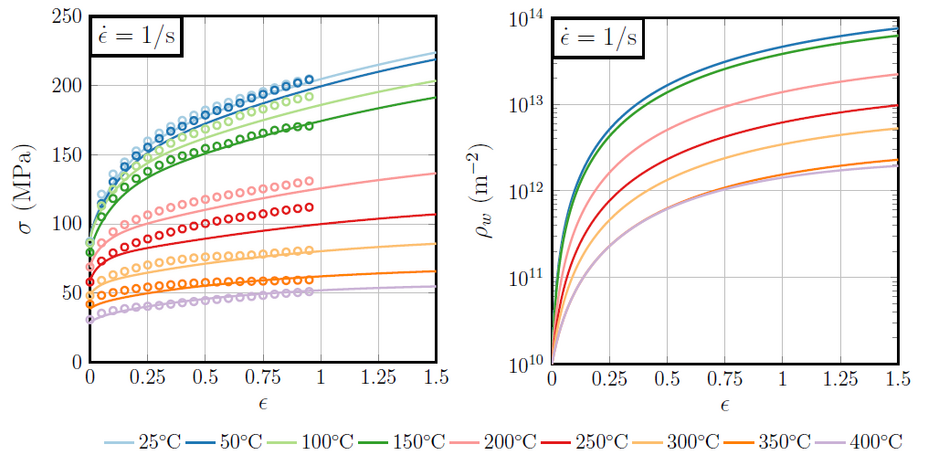
Amongst those mechanisms, strain hardening and recrystallization play a critical role, as they impact the production process as well as the material propperties.
Nowadays, aluminium and its alloys rank second in consumption volumes among metallic materials, surpassed only by steel. From packaging to transportation, in structural parts and facades or for decorative purposes, in the chemical industry, in construction, aluminium has become a key component in all kinds of applications. Especially, its low strength-to-weight ratio has been the primary factor for the development of the aeronautic and automotive industries.
General purpose alloys such as the 6082, based on the Al-Mg-Si system, are commonly found as sheets and extruded products, and are manufactured by a succession of thermo-mechanical steps designed to achieve the desired product characteristics.
Even though the design of technological alloys still relies heavily on experimentation, numerical microscopic models can provide a great deal of insight on the relationship between microstructure and macroscopic properties. For that reason, they are a tool on which industries and research departments rely more and more.
Strain hardening
During the rolling process, the mechanical strength of the material increases. It is then necessary to continuously raise the roll pressure in order to further deform the material. This physical phenomenon, known as strain-hardening, is a result of the rapid increase of microstructural defects in the material during plastic (permanent, in opposition to elastic) deformation. Taking into account the mechanisms by which crystalline line defects – called dislocations – multiply and annihilate, it is possible to design constitutive models able to relate the evolution of the flow stress of a material, i.e. the strain hardening, to its microscopic state.
Recrystallization
The defects accumulated in the microstructure under the form of dislocations and interfaces raise the energy stored within the material. Upon annealing, diffusion-controlled mechanisms are promoted. They allow the crystalline structure to recover and lower its energy by getting rid of the defects. Additionally, when the annealing temperature is high enough, new defect-free crystals can nucleate in the regions of high energy and grow into the deformed matrix – this phenomenon is called recrystallization. The radius of the fully grown crystalline grains depends on the level of deformation previously achieved, i.e. the amount of energy stored in the material, the annealing temperature and the eventual particles of second phase present in the microstructure.

Partially recrystallized microstructure after plain strain compression at room temperature and annealing at 300 °C for 20 minutes. The region of high strain recrystallizes first.
The influence of recovery on recrystallization is not trivial. It needs to be thoroughly taken into account in any recrystallization model. The latter usually feature an Avrami-type equation, which, when combined with a tailored nucleation model, becomes able to predict the recrystallization kinetics. Being able to forecast the grain structure is a critical matter for any manufacturer because it directly impacts several material properties, such as mechanical strength, solid state atomic diffusion, and crack propagation, etc.
Multiscale modelling
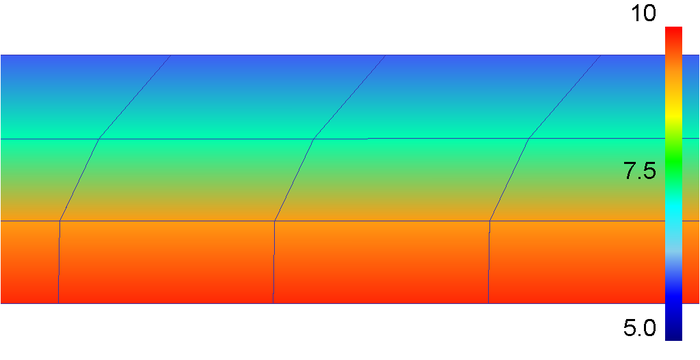
It has become a major concern of industries to model their production processes at multiple scales. The macroscopic scale is classically dealt with fairly well with a finite element model. By implementing the constitutive and recrystallization models in microscopic routines within the finite element framework, one can follow the various thermo-mechanical steps involved in the production of metallic plates. For instance, it is possible to calculate the stress involved in the deformation process, or predict the grain radius after continuous annealing at 550 °C. This project was made in collaboration with AMAG rolling Gmbh, TU Wien and the Austrian Institute of Technology.
2D-FE modelling of the rolling process with the constitutive model.
Financial support from the Austrian Federal Government (in particular from Bundesministerium für Verkehr, Innovation und Technologie and Bundesministerium für Wissenschaft, Forschung und Wirtschaft) represented by Österreichische Forschungsförderungsgesellschaft mbH and the Styrian and the Tyrolean provincial government, represented by Steirische Wirtschaftsförderungsgesellschaft mbH and Standortagentur Tirol, within the framework of the COMET funding programme is gratefully acknowledged.
Grain size distribution in the thickness of the plate after annealing at 550°C during 20s (in µm).