Another picture for download can be found at the end of the text
Though small and inconspicuous, they literally play a supporting role in the operational safety of high-voltage lines: insulator strings. They connect the live conductor to the overhead-line towers. Due to their low conductivity, they prevent the circuit from being closed via the towers and causing a short circuit. In addition, they bear the entire weight of the conductor together with additional load caused by wind or ice. The load exerted by an insulator string to the tower or its crossarm can exceed 40 tons (>400kN). If one strand of a multiple string breaks (so-called primary break), the remaining strands must absorb the highly dynamic impact in order to avoid a complete forced break. This is the only way to ensure that the necessary safety clearance to the ground can be maintained and that the conductor continues to hang securely from the tower. This is because if a 380kV overhead line conductor falls onto the neighbouring crossarm or onto the ground, this would be an immense risk.
First simulation of complex load redistributions
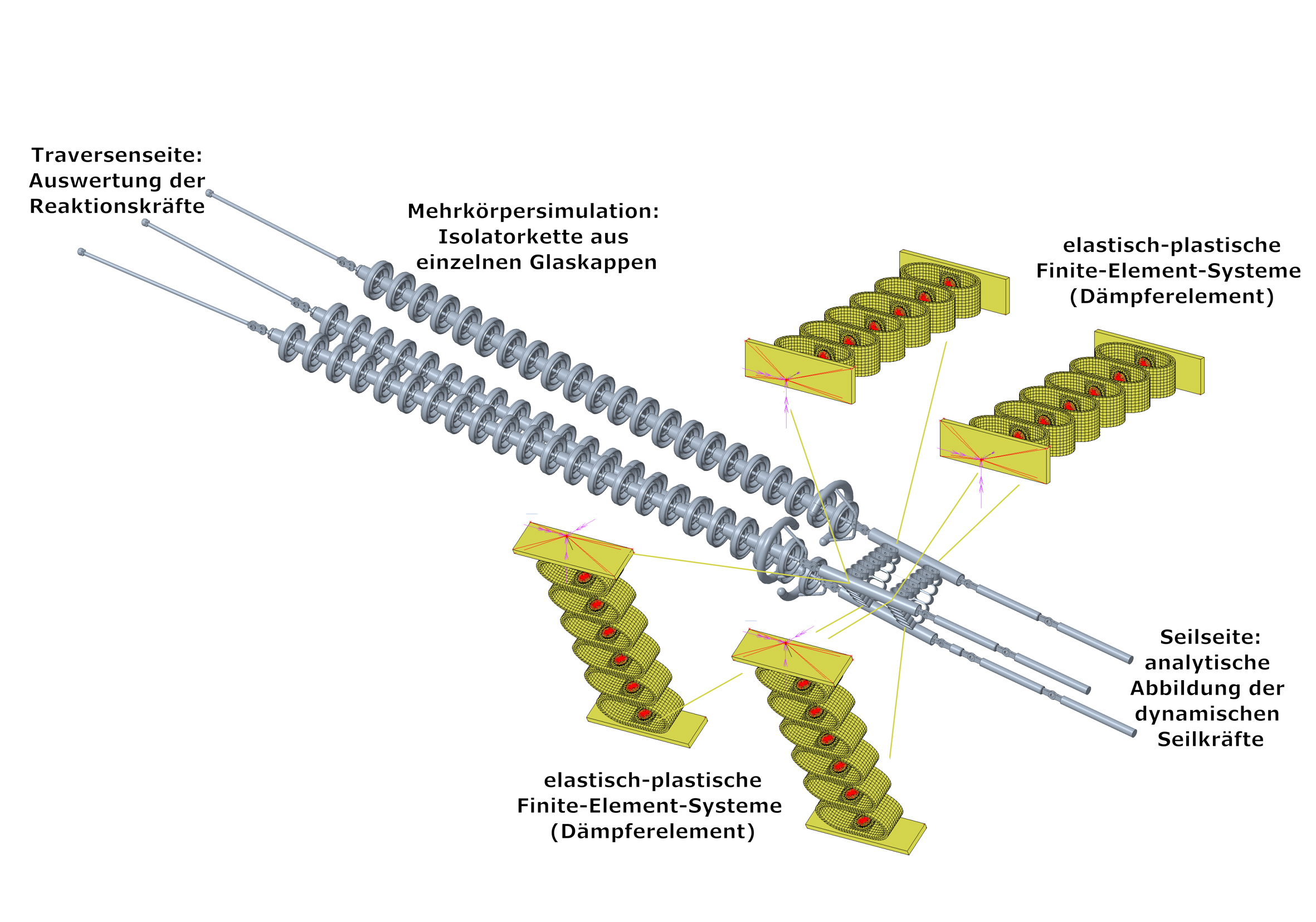
Christian Landschützer, a researcher at the Institute of Logistics Engineering at Graz University of Technology (TU Graz), and his team have simulated such highly dynamic load transfer processes – i.e. the process starting with the primary breakage of an individual insulator string, through the resulting oscillations, to the point at which all the conductor are at rest again. Under investigation were triple tension strings (i.e. three parallel insulator strands) of the Mosdorfer GmbH, from Weiz. Mosdorfer has installed an independently developed and patented damper element as a protective device in these strings. If an insulator strand breaks, the damping element is intended to reduce the shock-like load to a controllable level so that the remaining insulator strands do not also break, thus preventing the stranded conductor from falling due to this secondary break.
These were the first studies of their kind in the world. Previously, such simulations had only been carried out in a very simplified way. Plastic deformations were neglected or not mapped at all, since all components have been relatively stiff up to now. "Due to the third insulator strand and the damper element, we had to enter the three-dimensional realm for the first time and couple two simulation methods with each other. This is a level of detail that on the software side and due to the required computing power has only been possible at all for a few years," explains Landschützer and describes the further challenges: "In order to fully represent the load redistribution, we had to create a multi-body simulation model as well as models using the finite element method (Note: a numerical method for calculating the structural behaviour of individual object areas) and then couple them together so that they can calculate the highly dynamic process (this only takes about 0.2 seconds) in a time-synchronized manner." The cable dynamics and the movement behaviour of the insulator strands were modelled, and the plastic deformation of the damper element was mapped. The team from the Institute of Logistics Engineering simulated the breakage of all three insulator strands, both on the tower and on the conductor side, for each individual strand.
Reduced testing effort and cost savings
In the simulations, the researchers at the Institute of Logistics Engineering were able to show very precisely when and under what conditions different loads act on the insulator strands. As a result, these can now be utilized to a higher degree or dimensioned more leanly, since the loads are now better known from the simulation. Landschützer: "The bottom line is efficient material use and cost optimization in production."
However, costs are also saved at another level. Up to now, insulator strings have been tested in a single experimental facility of a unique type in Europe. The tests are carried out there on a one-to-one scale and cause additional (material) costs, while at the same time the number of test variants is severely limited. "Our results prove that the simulation method can replace costly experiments while maintaining the same quality, providing more flexibility and gaining more knowledge," says a pleased Landschützer. The engineer expects the method to be used in other applications in the future. He is inviting interested companies to contact the Institute of Logistics Engineering at TU Graz.
This research is anchored in the Field of Expertise "Mobility & Production", one of five strategic research areas of TU Graz.
