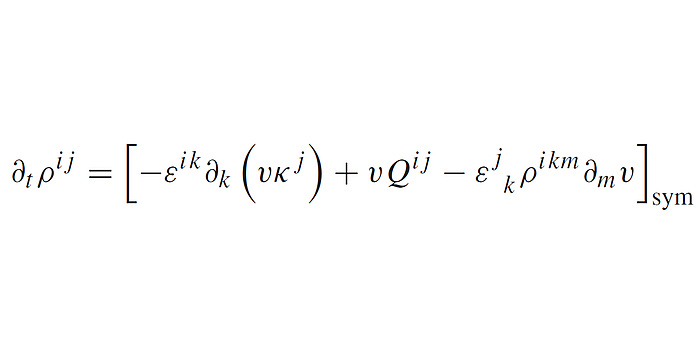So it is surprising that the plastic deformation of metals has not been completely understood by now. While elastic characteristics of new alloys may nowadays be predicted from quantum mechanical simulations, there is still no way to predict the plastic behavior of metals from basic properties of the crystal structure.
The plastic properties of metals are controlled by the presence and characteristics of line-like crystal defects, so-called dislocations. The motion of dislocations in response to stresses in the material are for several classes of crystal structures well understood. But metals typically contain a very large amount of dislocations. A cubic millimeter of a metal contains between 1 and 10,000 km (!) linelength of dislocations. Especially for metals with face-centered cubic crystal structure (e.g. austenitic steels and aluminum alloys) it is therefore the collective behavior of many dislocations rather than the characteristics of single dislocations which control the plastic characteristics. The hardening behavior during plastic deformation as well as the emergence of characteristic dislocation structures are both due to collective effects on the dislocation level. To understand the emergence of dislocation structures is of enormous economic importance because dislocation structures may initiate material failure when subject to alternating loads.
Continuum theories
In many areas of physics (diffusion, fluid mechanics, plasma physics) the continuum theories of engineering sciences may be derived from the behavior of many single objects using methods from statistical mechanics and thermodynamics. Such a derivation of a continuum plasticity theory from dislocation theory has long been viewed as a hopeless endeavour in materials science. One important reason for this is the fact that dislocations are moving flexible lines, which obstructs the application of methods from particle physics. Only recently, Thomas Hochrainer, Institute of Strength of Materials at TU Graz, laid the foundations for the transfer of the methods from particle physics. He adopted the concept of alignment tensors from other continuum theories of extended objects to the dislocation case and derived evolution equations for the tensorial dislocation density variables which account for the kinematics of moving flexible lines.
Schematic picture of the permanent shearing of a crystal produced by moving dislocations.
Within the Research Unit “Dislocation based plasticity” funded by the German Science foundation (DFG), with interdisciplinary partners at Karlsruher Institut für Technologie (KIT), Friedrich-Alexander-Universität Erlangen-Nürnberg and Technische Universität Bergakademie Freiberg, we are currently working on including collective effects due to dislocation interactions in the continuum dislocation dynamics framework. This requires transferring statistical mechanics and thermodynamics methods from many particle systems to the dislocation case.

Density plot of the total dislocation density in an early stage of dislocation pattern formation. Light grey means low density and dark grey high density. The orthogonal pairs of double-headed arrows indicate the local alignment of dislocations.
A surprising result from the continuum dislocation dynamics is the fact that the consideration of dislocation interactions naturally leads to the emergence of dislocation structures. The reason is that existing inhomogeneities get enhanced by a process similar to the emergence of traffic jams: where there is already a high dislocation density, dislocation becomes slowed down and contributes to a further accumulation of dislocations. Elastic interactions restrict the accumulation and determine the characteristic size of the emerging dislocation structures. The size of the structures was shown to scale as expected from experiments, that is, the size is proportional to the average dislocation spacing and inversely proportional to the applied stress.
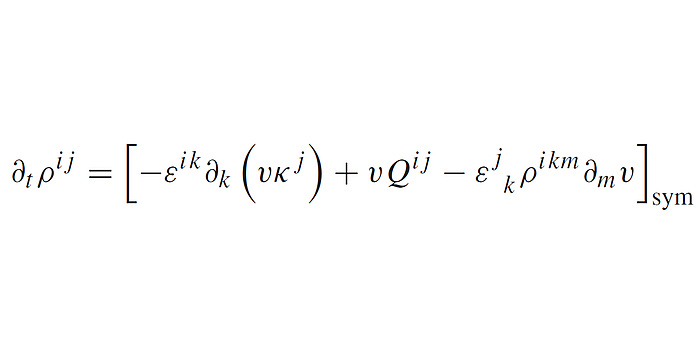
Evolution equation of the dislocation alignment tensor of second order.
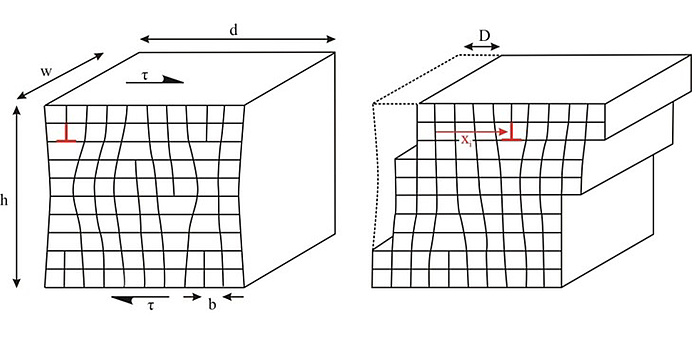
Due to the consideration of dislocation interactions, the continuum dislocation dynamics theory becomes moreover size-dependent. This means that for specimens with dimensions on the order of the average dislocation spacing, the plastic characteristics turn out to be dependent on the absolute size. Note that classical continuum plasticity is size-scale independent, but numerous size-effects have been observed in small-scale plasticity. We are currently in the course of validating the continuum dislocation theory by comparing it to micro-torsion experiments at KIT.
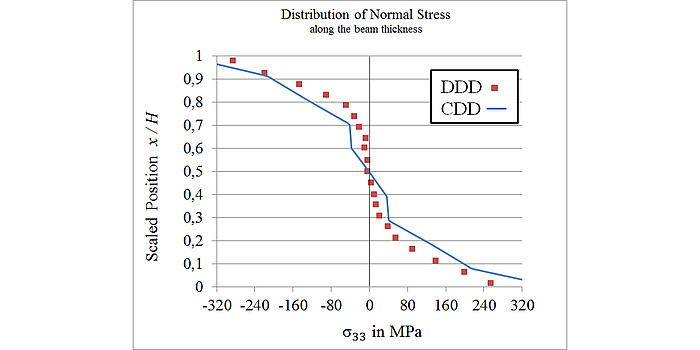
Longitudinal normal stress in a micro beam during bending. Solid line: results from continuum dislocation dynamics simulation. Red symbols: results from discrete dislocation dynamics simulations at KIT.
Future challenges
The next big challenge in continuum dislocation theory is predicting work hardening. This introduces new theoretical challenges because the dislocation reactions involved in strain hardening lead to dynamic changes of the topology of the dislocation network, which are not yet reflected in the current evolution equations.
This research project is attributed to the <link https: www.tugraz.at forschung fields-of-expertise advanced-materials-science ueberblick-advanced-materials-science _blank int-link-external of>Field of Expertise „Advanced Materials Science“ , one of TU Graz' five strategic areas of research.
Thomas HOCHRAINER
Univ.-Prof. Dipl.-Math.techn. Dr.-Ing.
Institute of Strength of Materials
Kopernikusgasse 24/1
8010 Graz
Phone: +43 316 873 7164
<link int-link-mail window for sending>hochrainer@tugraz.at
![[Translate to Englisch:] Eine blaue, schematische Darstellung einer Turbine.](https://www.tugraz.at/fileadmin/_processed_/0/1/csm_N_S_TUGrazresearch_2017_Plastizitaet_by_JustContributor-Fotolia_c9efe8f632.jpg)