Stochastic Optimisation in Financial and Insurance Mathematics

In risk management, being able to react to negative trends is essential. Resulting questions can be directly linked to stochastic optimisation problems.
Background
Financial and insurance mathematics is playing a prominent role in current probability theory. Its contributions are twofold: the analysis of practical problems is leading to deep theoretical findings, and results, which had been considered to be purely of a theoretical nature, are also feeding into applications. In research and the application of research findings, a distinction needs to be drawn between various aspects – or fundamental problems. One group of questions deals with the correct pricing of financial claims. In finance, the notion of a fair price broadly speaking dictates that a financial market should remain free of arbitrage after the introduction of a new product. Trading opportunities which lead to riskless profits should not arise. In insurance, however, the correct price of some newly insured risk should maintain the financial stability of an insurer.
The second class of problems puts the focus on portfolio and risk management. Typical problems in this context are concerned with the identification of investment strategies which maximise profit measuring functionals, or, conversely, minimisation of risk measures.
One aspect that both types of problem have in common is that underlying objects are modelled by probabilistic quantities. For example, in finance, prices of traded assets such as stocks, currencies or commodities are modelled as stochastic processes. However, in insurance it is crucial to describe claim events which are of a different nature in probabilistic terms.
I will outline two topics that I am currently investigating below.
Risk minimising investment
The chosen starting point is the situation of an economic agent (for instance an insurer) who is exposed to some fundamental risk which creates random fluctuations in its income stream. The resultant wealth generated needs to be invested in a financial market which is represented by a risky and a non-risky asset, for the sake of simplicity. The assets generate a low but deterministic and a higher but random interest return. Consequently, the division of wealth is under the control of the agent, who aims to minimize her shortfall probability, i.e. minimising the probability of having a negative wealth position at one point in time.
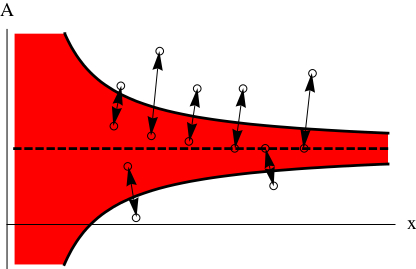
Figure 2
In typical portfolio problems, random fluctuations are modelled as Brownian motions and adaptions of the investment positions can be continuously implemented. To make the investment control more realistic, transaction costs are introduced into the model with the decisive effect that trading activities are limited to a discrete set of points in time. Optimal timing of interventions and optimal post-intervention positions for the two assets therefore need to be determined. The resulting stochastic optimisation problem is categorised as an impulse control problem. Its solution can be linked to a set of quasi-variational inequalities which involve a heat-equation type partial differential equation.
The theoretical and numerical results produced by this problem produce interesting phenomena. Firstly, they show that assuming an optimal additional risky position can be beneficial. This is demonstrated in Figure 1 in terms of survival probabilities (one minus the shortfall probability) where the red line corresponds to the case of fictitious continuous adaptions, the blue one to optimal impulses and the green curve to a purely non-risky investment. Secondly, the optimal strategy is a function of the total wealth position ‘x’ and the risky investment position ‘A’ (see Figure 2). The ideal continuous investment position is shown by the dotted line for reference. The strategy consists of jumps back to the red area whenever the (wealth/investment) position is too far from the ideal position. Here ‘too far’ is part of the problem’s solution and can be calculated by solving a free boundary value problem.
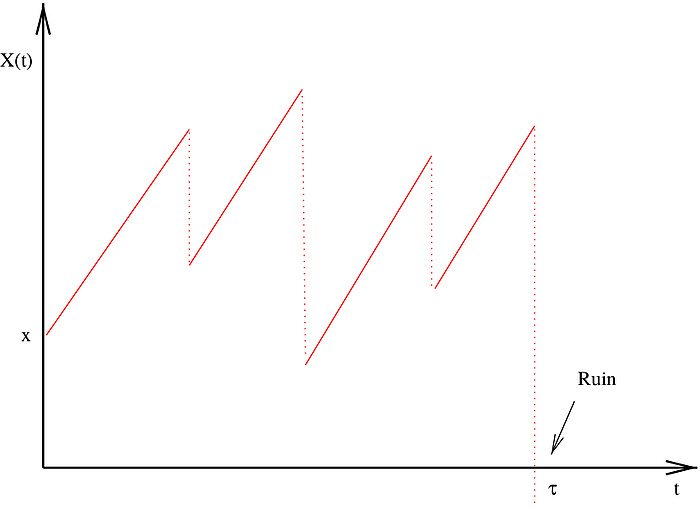
Figure 3
Optimal risk sharing
This problem deals with the construction of optimal reinsurance models for the minimisation of risk measures. Such models are risk sharing mechanisms between an insurer and a reinsurer – for a deterministic price the reinsurer assumes parts of claim payments.
The underlying model specifies the insurer’s surplus process by means of a continuous premium component and a jump process corresponding to claims, in general a piecewise-deterministic Markov process. Figure 3 illustrates a typical sample path. In mathematical terms, reinsurance changes the probability distribution of claims and the control problem focuses on its optimal choice. Fairly general penalty functions for the deficit can be considered as a risk minimisation measure. Solving the resulting problem relies on theoretical arguments which need to be supplemented by numerical results.
Figure 4 shows an iteratively determined numerical solution. The unbroken lines correspond to the expected penalty as a function of the initial surplus (the minimum in green), and the dotted lines represent the optimal risk sharing proportion which is also a function of the surplus.
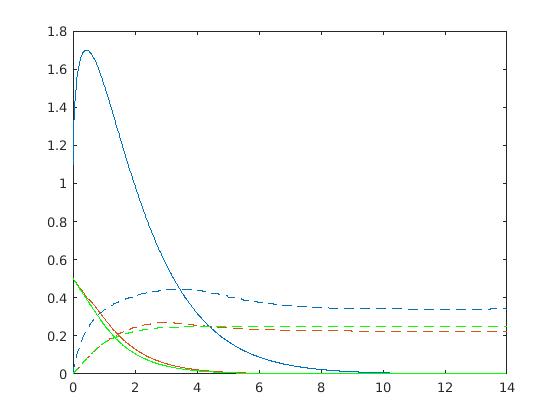
Figure 4
Kontakt
Stefan THONHAUSER
Assoc.Prof. Dipl.-Ing. Dr.techn.
Institute of Statistics
Kopernikusgasse 24/III
8010 Graz
Phone: +43 316 873 4540
stefan.thonhauser@math.tugraz.at




