Probabilistic Methods in Analysis and Number Theory

Basics
One of my research topics is metric number theory – a theory concerned with the properties of "typical" real numbers. Here one should note that in mathematics there are different sizes of "infinities", namely "countably infinite" and "uncountably infinite". A set is countably infinite if one could write down its elements on an infinite list one after another. The integers are of this cardinality, as are (somewhat surprisingly) the rational numbers, that is, fractions. In contrast, the real numbers (all numbers that can be written as an infinite decimal expansion) are uncountable – even on an infinite list one could not write all of them one after another. This might be somewhat irritating, and it probably does not come as a surprise that Georg Cantor, who developed this theory, met heavy resistance in the mathematical community at first (though his ideas are generally accepted today).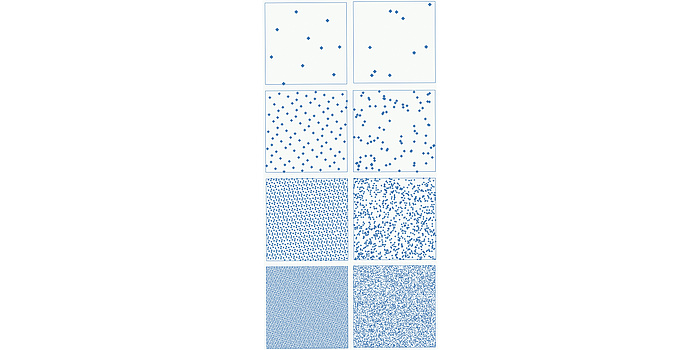
Practical application
Assume you want to calculate an integral, namely the average depth of a lake (yes, that is given by an integral). You cannot obtain a precise solution, so you need an approximation method. One possibility is the Monte Carlo method. Here, you take a large number of random points on the surface of the lake and determine the depth at these points, then the average depth of the lake will be roughly as large as the average depth at these sampling points. However, the size of the error will depend on the random choice of sampling points – where it is not clear how "random" points can actually be chosen. Another method is the quasi-Monte Carlo method. Here, rather than taking random sampling points, you take carefully chosen (non-random) sampling points. One can show that this method often performs much better than the Monte Carlo method. Now imagine that rather than a two-dimensional integral (such as the average depth of the lake) you want to calculate a 1000-dimensional integral. That may sound absurd, since everybody knows that the "real world" is only three-dimensional. However, highdimensional integrals are extremely important for applications – for example, if you want to calculate the expected loss in an insurance contract for 1000 insured persons, then mathematically this is a 1000-dimensional integral. Again, the quasi-Monte Carlo-method can give very good results – but many questions are still open, including very partial question such as: up to which size can the quasi-Monte Carlo method be efficiently implemented on a computer? What happens when the number of dimensions is increased? Can I only integrate simple functions or also irregular ones?
This research project is attributed to the <link https: www.tugraz.at en research fields-of-expertise information-communication-computing overview-information-communication-computing _blank int-link-external external link in new>Field of Expertise "Information, Communication & Computing", one of TU Graz' five strategic areas of research.
Kontakt
Assoc.Prof. Dipl.-Ing. Dr.techn.
Institute of Analysis and Number Theory
Kopernikusgasse 24/II
8010 Graz
Tel.: +43 316 873 7127
<link int-link-mail window for sending>aistleitner@math.tugraz.at



