Probabilistic Methods in Analysis and Number Theory

The hearings for the FWF START Prize took place in rooms of the Austrian National Bank. After some waiting time, during which the nominees could entertain themselves by visiting the huge exhibition, the hearings only took a few minutes. The phone call from the steering committee of the FWF soon informed me that our project had been granted. Initially I was relieved – because only ten per cent of the nominees are granted an award. My project is split into two parts, one of a more fundamental nature concerning questions on analysis and number theory, and one concerning questions arising from "real-world" applications of mathematics.

Basics

One of my research topics is metric number theory – a theory concerned with the properties of "typical" real numbers. Here one should note that in mathematics there are different sizes of "infinities", namely "countably infinite" and "uncountably infinite". A set is countably infinite if one could write down its elements on an infinite list one after another. The integers are of this cardinality, as are (somewhat surprisingly) the rational numbers, that is, fractions. In contrast, the real numbers (all numbers that can be written as an infinite decimal expansion) are uncountable – even on an infinite list one could not write all of them one after another. This might be somewhat irritating, and it probably does not come as a surprise that Georg Cantor, who developed this theory, met heavy resistance in the mathematical community at first (though his ideas are generally accepted today).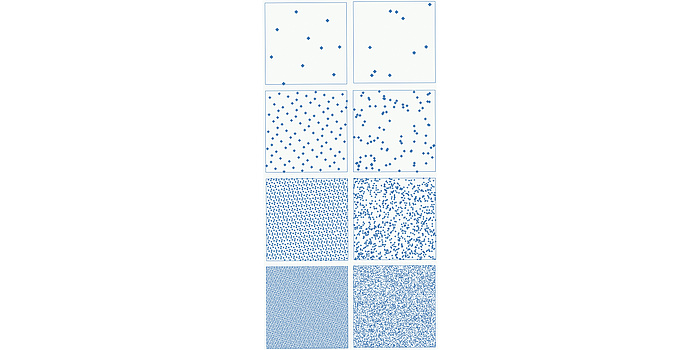To come back to metric number theory: since we now know that there are very many real numbers, it does not make sense to investigate them one after another, instead it makes sense to find properties which hold for all "typical" (in a very precise sense) real numbers. For example, a typical real number has as many zeros in its decimal places as it has ones. If any of this does not make any sense to the reader, then at least he will believe that such questions are of a rather fundamental nature and somewhat detached from the so-called real world. For the mathematician this is not a problem. However, if many many different mathematical areas come together in a mathematical field (such as in our case number theory, Fourier analysis, probability theory and ergodic theory) and little by little one comes to realize the hidden connections between different phenomena, then this gives the mathematician great pleasure.

Practical application

Assume you want to calculate an integral, namely the average depth of a lake (yes, that is given by an integral). You cannot obtain a precise solution, so you need an approximation method. One possibility is the Monte Carlo method. Here, you take a large number of random points on the surface of the lake and determine the depth at these points, then the average depth of the lake will be roughly as large as the average depth at these sampling points. However, the size of the error will depend on the random choice of sampling points – where it is not clear how "random" points can actually be chosen. Another method is the quasi-Monte Carlo method. Here, rather than taking random sampling points, you take carefully chosen (non-random) sampling points. One can show that this method often performs much better than the Monte Carlo method. Now imagine that rather than a two-dimensional integral (such as the average depth of the lake) you want to calculate a 1000-dimensional integral. That may sound absurd, since everybody knows that the "real world" is only three-dimensional. However, highdimensional integrals are extremely important for applications – for example, if you want to calculate the expected loss in an insurance contract for 1000 insured persons, then mathematically this is a 1000-dimensional integral. Again, the quasi-Monte Carlo-method can give very good results – but many questions are still open, including very partial question such as: up to which size can the quasi-Monte Carlo method be efficiently implemented on a computer? What happens when the number of dimensions is increased? Can I only integrate simple functions or also irregular ones?Of course, the actual research topics in our project are much more focused, and much more complex as well. I am working in this project together with two postdoc researchers and one PhD student. All three positions were advertised internationally, and in all three cases there was a very large number of (qualified) applicants. For me this is a clear confirmation that the TU Graz is an attractive place for young international scientists.

This research project is attributed to the Field of Expertise "Information, Communication & Computing", one of TU Graz' five strategic areas of research.