Nowadays, electrical machines are ubiquitous in our lives. In order to design machines which – depending on the concrete application – perform as well as possible, mathematical methods for the optimization of the geometry of the machines can be used. These methods can yield designs which one might not have expected beforehand.
Electrical machines have become an integral part of our everyday lives. Whenever we put a plug into a power socket and thereby initiate the movement of a device – be it a blender, a vacuum cleaner or a washing machine – there is an electric motor involved (see Figure 1) which converts electrical energy into mechanical energy. Electric motors are almost indispensable also in industrial applications as industrial electric motors consume more than 40% of the electrical energy produced worldwide. Therefore, it is obvious that the optimization of such electrical machines has a large potential for saving energy.
When designing electric motors, besides answering fundamental questions about the type, size or materials used, the exact shape of the motor which allows for an ideal magnetic flux also has to be determined. Since the magnetic flux is better in iron than it is in air regions of the motor, it is possible to guide the flux in a desired way by introducing holes or air regions in a smart way (see Figure 2). In this way, the overall performance of the motor can be influenced. This design process is often done based on the intuition and experience of electrical engineers. Additional optimization with respect to geometric parameters, such as lengths or orientations of parts of the motor, can further improve its performance. However, this kind of optimization can only yield designs which are of the same type as the chosen initial design.
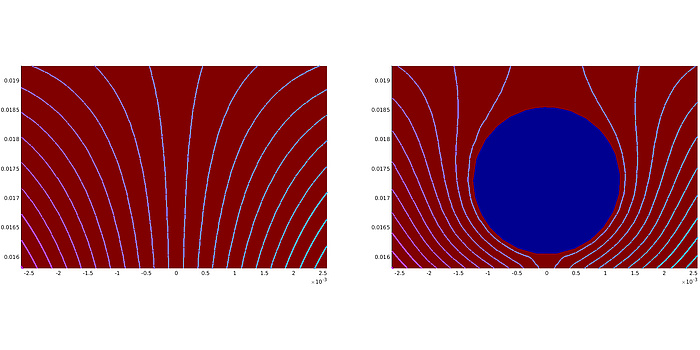
Figure 2: Magnetic flux in iron without and with air hole.
In my research, I am dealing with the question of how to choose the inclusions of air (or the distribution of material) inside a motor in an optimal way, e.g., such that the motor achieves a torque which is as high as possible or such that it rotates as smoothly as possible. Here, there should not be any restrictions on the shape and number of air inclusions, allowing for new and innovative designs to arise. This practical task can be reformulated into a mathematical problem of shape or topology optimization. Thus, the task is to find the shape of a domain Ω (representing a certain part of the electric motor) which maximizes a given objective function (e.g. torque or smoothness of rotation).
For this optimization problem, the unknown is not a vector of real numbers or a function in a function space, but a set Ω which represents the geometry of a part of the motor (see Figure 3 left). In particular, here we do not have a vector space structure and, therefore, cannot simply add or subtract two sets. In order to utilize gradientbased optimization methods, we need sensitivity information, i.e. information about the change of the objective function when the set Ω changes. We distinguish between two kinds of geometry changes: on the one hand, the deformation of the boundary of a domain in the direction of a vector field (see Figure 3 center), and on the other hand the modification of the geometry by the introduction of a hole in the interior (see Figure 3 right). The corresponding sensitivities are called shape derivative and topological derivative, respectively. Using this information, it is possible to gradually improve the geometry until a (locally) optimal design has been reached. In topology optimization, one could introduce a small hole in every optimization step at that position where the topological derivative attains the largest value. Similarly, using the shape derivative it is possible to determine in every iteration a vector field which yields an improvement of the objective function when deforming the domain Ω in the direction given by this vector field.
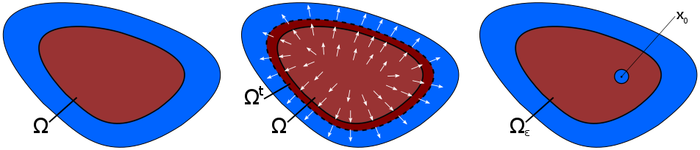
Figure 3: Set Ω representing the iron parts of the electric motor (left). Deformation of Ω in direction of a vector field (center). Modification of Ω by introduction of air hole (right).
Figure 4 (right) shows the result of a combination of these two approaches. Starting out from the design in Figure 4 (left), the design areas are modified in such a way that the rotation of the motor is as smooth as possible. We can see that, in this way, we could find new optimized machine designs without any expertise in electrical engineering, just using geometric sensitivity information. In order to obtain designs which can be used in practical applications in industry, several additional factors would have to be included. Usually it is not enough to perform optimization only with respect to one objective functional. For instance, in addition to the electromagnetic performance of the motor, we would also have to consider its production cost. Then, there is usually not one optimal solution, but a set of Pareto optimal designs. Further quantities of interest include the mechanical stability, the thermal behavior and also the manufacturability of the optimized design. Moreover, the optimized design, which was created in a computer model, should be robust with respect to small perturbations as they appear during the production process.We see that the topic of optimizing electrical machines can be seen as a mathematical playground connecting a number of mathematical and technical disciplines which still offers enough challenges for further mathematical and interdisciplinary research.
Figure 4: Initial geometry (left) and optimized design (right) with maximally smooth rotation.
