Adaptierung eines Phasenfeldmodells für Leerstellendiffusion und Analyse anisotroper Gradientenenergien in fcc-Kupfer-Einkristallen
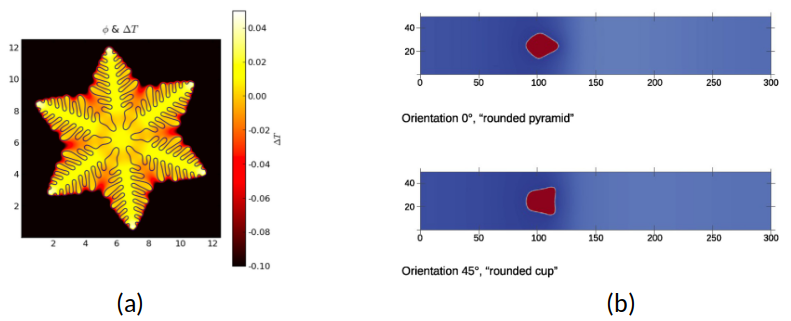
(b) Einfluss der Materialorientierung auf Porenmorphologie [2]
In der Phasenfeldmodellierung der Erstarrung – einschließlich des Dendritenwachstums – sind richtungsabhängige Gradientenenergien seit Langem etabliert, um Morphologie und Wachstumsdynamik realistisch abzubilden. Diese Methodik bietet eine natürliche Vorlage für defektgetriebene Phasenfeldmodelle. Da fcc-Kristalle eine kubische Anisotropie aufweisen, ist davon auszugehen, dass solche Anisotropien auch Leerstellendiffusion, Nukleation sowie Porenbildung und -wachstum beeinflussen.
Im Zuge dieser Arbeit soll die für ein analoges Modell [2] hergeleitete und angewandte Formulierung einer kubisch-anisotropen Gradientenenergie in die freie Helmholtzenergie eines Referenzmodells [3] integriert werden. Das Phasenfeldmodell in [3] nutzt bisher eine isotrope Gradientenenergie mittels eines skalarem Koeffizienten. Die Auswirkungen dieser Adaption auf das Porenwachstum sollen systematisch untersucht und mit dem isotropen Referenzfall verglichen werden. Im Fokus stehen die Orientierungsabhängigkeit von Porenformen im Zusammenspiel mit Materialorientierung und der Einfluss von mechanischer Belastung (elastische Kopplung). Die Ergebnisse sollen qualitativ (Morphologie, Richtungsabhängigkeiten) und quantitativ (Wachstumsraten, effektive Oberflächenenergien) ausgewertet werden.
[1] J. E. Guyer, D. Wheeler, J. A. Warren (2025, September 30). examples.phase.anisotropy. FiPy (NIST). pages.nist.gov/fipy/en/latest/generated/examples.phase.anisotropy.html
(Zugriff am 17.10.2025)
[2] J. Kundin et al. Modeling vacancy-induced porosity in compositionally-graded complex alloys. Acta Mater., 271 (2024)
[3] K. A. Pendl and T. Hochrainer. Coupling stress fields and vacancy diffusion in phase-field models of voids as pure vacancy phase. Comput. Mater. Sci., 224 (2023)
Aufgaben:
• Literaturrecherche zu Phasenfeldmethoden (für Poren/Leerstellen) mit Schwerpunkt anisotrope Gradientenenergien (kubische Symmetrie, Formfunktionen)
• Implementierung erster einfacher Codes (z.B. MATLAB/Python) zur Analyse/Visualisierung von Anisotropiefunktionen und ihrer Normalen-/Krümmungsabhängigkeit.
• Einarbeitung in vorhandene Simulations-Codes (Modell aus Quelle [3]) und Adaptierung auf Anisotropie (Austausch/Erweiterung des Gradientenenergieteils, konsistente Variation).
• Simulation von Diffusionstests unter mechanischer Belastung, Auswertung von Porenform, Orientierungseffekten und Wachstumsraten; Vergleich isotrop vs. anisotrop.
• Validierung der Ergebnisse (Konvergenz-/Netz-Studien, Literaturtrends)
• Dokumentation der Ergebnisse
• Optional: Analyse nicht-klassischer Nuklei bei anisotropen Energien
• Optional: Analyse anisotroper Mobilitätseffekte (richtungsabhängige Diffusionsmobilität) und deren Zusammenspiel mit der anisotropen Gradientenenergie.
Was Sie mitbringen sollen:
• Lehrveranstaltungen „Höhere Festigkeitslehre“ (VO und/oder UE) von Vorteil, optional LVs wie „Laborübung FE-Methoden“, oder „Rechnerübung Nichtlineare Festkörpermechanik“
• Interesse an Festkörpermechanik und gekoppelten Problemstellungen
• Programmiererfahrung (mit einer beliebigen Programmiersprache) vorteilhaft
Was wir Ihnen bieten:
• Intensive Betreuung am Institut
• Einarbeiten in numerische Algorithmen und Anwenden von theoretischem Wissen
Beginn: ab sofort möglich
Kontakt: Dipl.-Ing. Dr.techn. Kevin Pendl BSc kevin.pendl@tugraz.at
Betreuer: Univ.-Prof. Dipl.-Math.techn. Dr.-Ing. Thomas Hochrainer & Dipl.-Ing. Dr.techn. Kevin Pendl BSc
