Adapting a Phase-Field Model for Vacancy Diffusion and Analysis of Anisotropic Gradient Energies in FCC Copper Single Crystals
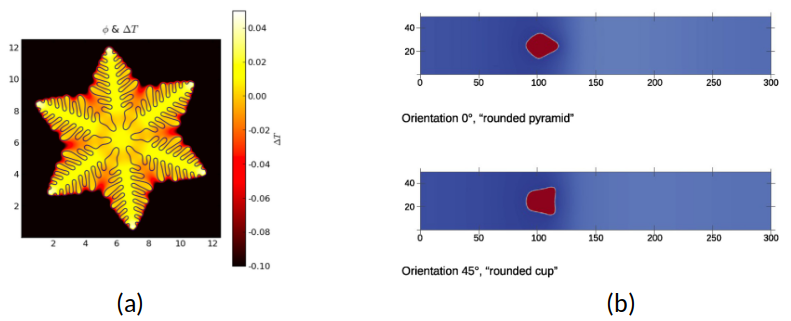
(b) Effect of crystal orientation on void morphology [2]
In phase-field modeling of solidification – including dendritic growth – direction-dependent (anisotropic) gradient energies have long been established to realistically capture morphology and growth dynamics. This methodology provides a natural template for defect-driven phase-field models. Because FCC crystals exhibit cubic anisotropy, such anisotropies are expected to influence vacancy diffusion, nucleation, and void formation and growth.
In this thesis, the formulation of a cubic-anisotropic gradient energy developed and applied in an analogous model [2] will be integrated into the Helmholtz free energy of a reference model [3]. The phase-field model in [3] currently uses an isotropic gradient energy via a scalar coefficient. The effects of this adaptation on void growth will be investigated systematically and compared against the isotropic reference case. The focus is on the orientation dependence of void shapes in combination with material (crystal) orientation and on the influence of mechanical loading (elastic coupling). Results will be evaluated qualitatively (morphology, directional dependencies) and quantitatively (growth rates, effective surface energies).
[1] J. E. Guyer, D. Wheeler, J. A. Warren (2025, September 30). examples.phase.anisotropy. FiPy (NIST). pages.nist.gov/fipy/en/latest/generated/examples.phase.anisotropy.html
(Zugriff am 17.10.2025)
[2] J. Kundin et al. Modeling vacancy-induced porosity in compositionally-graded complex alloys. Acta Mater., 271 (2024)
[3] K. A. Pendl and T. Hochrainer. Coupling stress fields and vacancy diffusion in phase-field models of voids as pure vacancy phase. Comput. Mater. Sci., 224 (2023)
Tasks:
• Literature review on phase-field methods for voids/vacancies with an emphasis on anisotropic gradient energies (cubic symmetry, shape functions)
• Implementation of simple scripts (e.g., MATLAB/Python) to analyze/visualize anisotropy functions and their dependence on surface normal and curvature
• Familiarization with existing simulation codes (model from source [3]) and adaptation to anisotropy (replace/extend the gradient-energy part with a consistent variational treatment)
• Diffusion tests under mechanical loading; evaluation of void shape, orientation effects, and growth rates; comparison of isotropic vs. anisotropic cases
• Validation of results (convergence/mesh studies, comparison with trends in the literature)
• Documentation of the results
• Optional: Analysis of non-classical nuclei under anisotropic energies
• Optional: Analysis of anisotropic mobility effects (direction-dependent diffusion mobility) and their interplay with the anisotropic gradient energy
What you should bring:
• Finished institute courses „Finite element method“ (lecture and/or practical) are beneficial, optional courses such as „Laboratory tutorial: finite element methods“ or „Computer lab: nonlinear solid mechanics“ are a plus. Our institute’s courses are ideal, but equivalent coursework elsewhere is welcome.
• Interest in solid mechanics and coupled field problems
• Programming experience (in any language) is an advantage
What we offer:
• Close, hands-on supervision at the institute
• Training in numerical algorithms and the application of theoretical concepts
Start: available immediately
Contact: Dipl.-Ing. Dr.techn. Kevin Pendl BSc kevin.pendl@tugraz.at
Supervisors: Univ.-Prof. Dipl.-Math.techn. Dr.-Ing. Thomas Hochrainer & Dipl.-Ing. Dr.techn. Kevin Pendl BSc
