SIGMACADE

One of the major problems in engineering is still the gap between computer aided design (CAD) and simulation, referred to as Computer aided engineering (CAE). This gap results from different representations used for the CAD, based on exact geometries like NURBS or subdivision surfaces, and for CAE, based on approximative mesh representations, the finite element model (FEM). Isogeometry refers to the extension of the standard FEM to more general basis functions common in CAD approaches. By circumventing many of the problems that are encountered during the mesh generation process by working directly with the CAD model, isogeometric analysis effectively eliminates the geometric error component of the analysis pipeline. Geometric refinement is no longer necessary, the analyst can focus attention solely on the solution refinement. In this project we explore a unified framework based on the subdivision surface representation. The main advantage of subdivision surfaces is their ability to model arbitrary geometry with one single surfaces, resulting naturally in a watertight mesh necessary for analysis. For the exploration of subdivision surfaces as a unified framework for both CAD and CAE we choose the SubDNURBS algorithm, a subdivision algorithm first presented at SIGGRAPH 2009. This subdivision representation is compatible with NURBS (non-uniform, rational B-splines), the current IGES standard, and Catmull-Clark subdivision surfaces. This subdivision representation enables the exploration of non-uniform knots and arbitrary degree in an isogeometric analysis approach. The aluminum can deforms in response to prescribed displacements of the top and bottom vertices. The pattern of deformation observed in the simulation result resembles deformations typically observed in real world examples.

Results

Comparison to analytic solutions

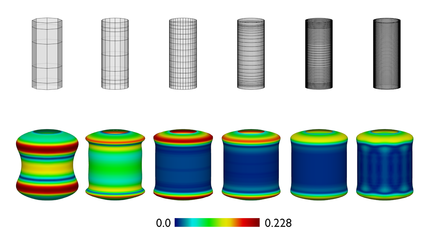Comparison of SubDNURBS simulation results to analytic reference solutions using different mesh densities. Colouring of the solution serves as an indicator of error between simulation results and analytic solution. The denser the control mesh, the better the simulation compares to the analytic solution.

Higher degrees

Using higher degree SubDNURBS gives better results for the same (low resolution) control mesh.

Non-uniform knot vectors

Non-uniform knot vectors allow for more control over the limit surface. Both simulations are based on the same control mesh. However, the right mesh has a different knot vector chosen at one of the edges, changing its shape slightly. Numerical analysis shows that this slight change will affect its stability considerably.

Deformation of complex geometry

Unlike NURBS based isogeometric analysis, isogeometric analysis based on subdivision can handle arbitrary topology.

Structural analysis of real world geometry

Comparing different roof profiles Isogeometric analysis allows to peform analysis of real world geometry directly on the CAD mesh. Simulation of a real roof      This modern tent-roof consists of a single subdivision surface which can be directly used for simulation. Reference: Riffnaller-Schiefer, A., Augsdörfer, U., and Fellner, D. 2016. Isogeometric shell analysis with NURBS compatible subdivision surfaces. Applied Mathematics and Computation 272, Part 1, 139–147.
View publication

This project was made possible by a Marie-Curie Fellowship.