Effect of Load Path on Failure

Failure and instability are key interrelated phenomena that govern the mechanical behavior of material and structural systems. Failure is most appropriately described as a sequence of events which progressively take the material from the initial stable state into an unstable and discontinuous state. The essential feature of a material system at failure stage is that it cannot continue bearing further load which is often characterized by its inability to sustain higher stress (i.e. σ̇_ij­ = 0).

Consequently, the failure criterion may be defined as singularity of stiffness tensor. However, in practice, most commonly, failure criteria are described as a general function of the stress tensor acting on the material, which in its most general case can be written as F(σ_ij) = 0. As it is obvious from this function form, at any point during the loading, the current state of stress tensor is used to decide whether or not failure has happened. However, this seems to contradict the above definition of failure as a progressive process of events taking the material into an unstable configuration.

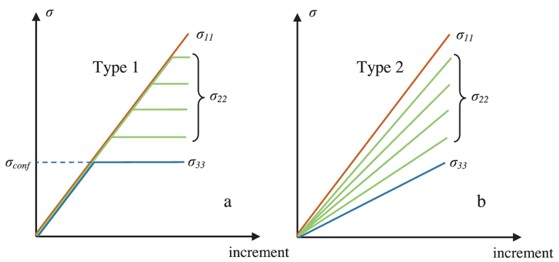
We have developed a series of loading-paths that are different from the classical loading paths of testing material strength in order to test this idea. The classical loading path used for deriving failure stress is shown as Type 1 in Figure 1.a. In this path, it is seen that all three components of principal stress are increased at the same rate initially until a desired level of hydrostatic confinement is reached. Afterwards one of the stress components, say σ₃, is kept constant and the two others are increased at the same rate. Then σ₂ is also kept constant at some point and σ₁ is increased until failure is reached. This experiment is repeated for different final values of σ₂. These experiments are specifically designed to check whether failure stress depends on the intermediate component of principal stress, σ₂(most failure criteria used in practice assume failure to be independent of σ₂). Experimental measurements done in Stanford, Northwestern, and Wisconsin universities as well as simulation results published by us show that σ_1(failure) clearly depends on the final value of σ₂. The second loading path I designed, shown in Figure 1.b, is designed specifically to demonstrate the effect of loading path on material behavior, and specifically, on failure. In loading of Type 2, the material is loaded simultaneously in directions 1, 2, and 3, but with different rates. These rates are defined such that the stress states would reach the stress components at the point of failure in loading of Type 1. Our calculations, performed with Granular Micromechanics Approach (GMA) is shown to be able to, not only, capture the results of experiments with remarkable accuracy, but also predict results of further experiments.

In the proposed project, we will use the GMA code for modeling additional loading paths and showing the effect of loading path on failure stress state as well as the direction of failure. More importantly, we will study the average behavior of inter-particle contacts in different directions to derive interesting insights into the microscopic behavior of the material through different loading scenarios. These results are of great importance in (1) predicting the behavior of materials under various loading scenarios (2) designing new materials – metamaterials – tailored to the loading that they are going to endure (3) topology optimization of structures by using the materials in regions that undergo the appropriate loading path in which they can leverage their full potentials.

Requirements:

• Ability to work with MATLAB
• Basic knowledge of strength of materials and solid mechanics
• Passionate to learn new topics in the area of micromechanical material modeling and publishing results

Our offer:

• Mentoring of the whole Master thesis at the institute
• Promising research topic
• Participation in fundamental research with wide ranging applications in different fields
• Presentation of your work in international conferences

Contact:
TU Graz, Institute of Strength of Materials
Payam Poorsolhjouy, PhD
+43 (0)316 873 7664
payam.poorsolhjouy@tugraz.at