Multiphysics: Modelling and simulation

The modelling of mechatronic systems leads to so called multifield problems, which are described by a system of nonlinear partial differential equations. The complexity consists of the simultaneous computation of the involved single fields as well as in the coupling terms, which introduce in most cases additional nonlinearities, e.g. moving/deforming conductive bodies within an electromagnetic field. For the efficient solution of these multifield problems, we have developed within the last years the simulation software openCFS, which allows high-end computations of the following coupled fields: electromagnetics-mechanics-acoustics, piezoelectrics-acoustics, electro-thermo-mechanics, electrostatic-mechanics-acoustics, and aeroacoustics.

In the following three courses, we teach from the basics to the current state of art the physical modelling and numerical simulation using the Finite Element (FE) method for coupled field problems and its practical application to complex technical and medical systems, are introduced.

Methods of Simulation of Mechatronic Systems (437.223/224)

The calculation of the potential distribution of e.g. an arrangement of electrically charged electrodes by means of analytical methods only leads to closed analytical expressions for very few arrangements (e.g. spherical or cylindrical electrodes). For the multitude of such problems with arbitrary geometries of the electrodes, no closed analytical solution can be found. The same applies to problems in the field of steady-state current flow or static magnetic fields. Nevertheless, in order to determine field distributions or integral quantities such as the energies stored in the field, numerical methods such as the finite element method (FEM) are the methods of choice. In this lecture, the basics of the FE method are elaborated.

The introductory chapter deals with the calculus of variations, the variational method in mechanics, the principle of least action and Lagrange's method. In the second chapter, the variational method is applied to a static electric field problem and, finally, Ritz's method is discussed. The third chapter deals with the method of weighted residuals, which, in contrast to Ritz's method, leads to a numerical approximate solution without the need of a so-called functional. The corresponding boundary conditions are also discussed in the second and third chapters. The fourth chapter deals with the finite element method. In particular, a two-dimensional nodal element formulation is discussed in details using the example of a static electric field problem. Chapter five is devoted to isoparametric FE and the construction of higher order shape functions. Chapter six applies what has been learnt to plane and rotationally symmetric problems from the fields of electrostatics, the steady state current flow and the static magnetic field induced by a steady state current.

Multiphysical Simulation I (Multiphysical Models in Mechatronics, 437.233/234)

In general, physical quantities describing the effects in coupled field problems are a function of space and time, and the description leads to a system of partial differential equations (PDEs). In general, these PDEs cannot be solved analytically and require the application of numerical methods such as the finite element (FE) method. In this course the basic approach to solve coupled field problems using the finite element method is taught. In detail the mathematical / physical relationships as well as their finite element formulation of the following coupled field problems are discussed: (1) electric flow field-heat conduction- mechanics (forward coupling); (2) piezoelectricity (direct volume coupling between electrostatic and mechanical field); (3) mechanics-acoustic (interface coupling). In the exercise course, students will independently perform simulations of practically relevant coupled field problems with openCFS: power semiconductors, piezoelectric bimorph actuator, sound radiation of a loudspeaker. The students are interactively supervised in the execution of the tasks.

Heat sink (left), Piezoelectric bimorph actuator (middle), Electrodynamic loudspeaker (right)
 

Multiphysical Simulation II (Multiphysical Simulation, 437.235/236)

Based on the course Multiphysical Simulation I we extend the complexity and discuss the physical modelling and numerical simulation of physical fields including nonlinearities and coupled fields with nonlinear coupling terms. Thereby, we focus on coupled electromagnetic-mechanical systems (e.g. electromagnetic valves in automotive injection systems, coupled electromagnetic-heat systems (e.g. induction heating by eddy currents), and aeroacoustics (e.g. human voice being generated by flow induced sound). In addition, we provide latest Finite-Element (FE) formulations for non-conforming grid techniques and higher order finite elements. In the interactively supervised exercise course, students will perform simulations of practically relevant applications in technical and medical science.

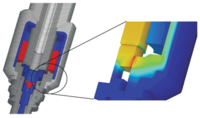
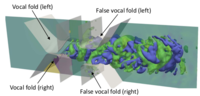
Electromagnetic valve (left), Induction heating (middle), Sources of human voice in larynx (right)