Electromagnetic fields

The theory of electromagnetism, known as classical electromagnetism, has been unified by James Clerk Maxwell resulting in four fundamental equations, known as Maxwell's equations, and the electromagnetic force described by the Lorentz force law. Significant extensions took place through the theory of relativity (closely related to electrodynamics) and quantum electrodynamics (electromagnetic fields are waves and particles at the same time). In the following courses, we provide a systematic description of all main phenomena in electromagnetics, and discuss mathematical methods for the analytic and the numerical solution.

Electrodynamics (437.255/256 as well as 437.163/164)

This course discusses the behaviour of electromagnetic fields and their interactions applying analytical solution methods. In doing so, Maxwell's equations are presented in their differential and integral form using vector operators gradient, divergence and rotation as well as integral theorems of Gauss and Stokes. The vector operators allow a short representation of Maxwell's equations, independent of the choice of coordinate system, from which new equations can be derived with the help of vector analysis. Electromagnetic fields are divided into the following classes, which are discussed one after the other: electrostatics both in vacuum and polarisable materials, static electric flow field, magnetostatics both in vacuum and magnetisable materials, quasi-static electromagnetic field (eddy current case) and full Maxwell equations. For all physical quantities (electric field intensity, dielectric displacement, electric scalar potential, magnetic flux density, magnetic field intensity, magnetic vector potential) we discuss their fundamental equations, analytical solution approaches and transmission conditions. In addition, we discuss the computation of energy and force.

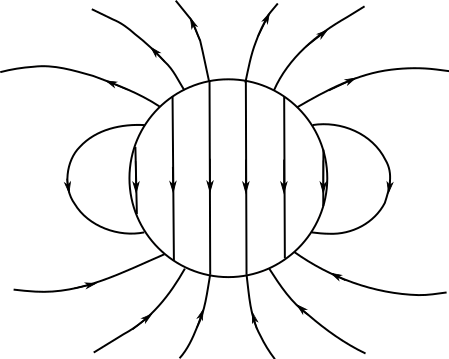
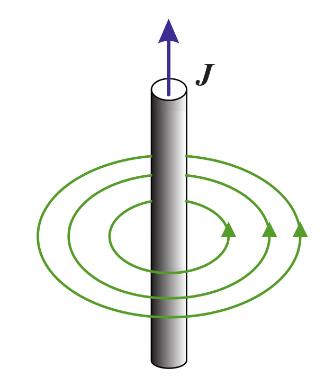
Electric field lines of a polarized sphere (left), Magnetic field lines around a current carrying conductor (right)

Basic Experiments in Electrodynamics, Laboratory (437.141)

Beside some very basic measurements on DC and AC circuits discussing the stationary behaviour as well as transient observations in specific circuits also experiments showing force effects of electromagnetic fields are conducted.

More specifically the Helmholtz superposition principle in combination with the development of so called Norton and Thevenin equivalent sources on a complex circuit is solidified in this laboratory exercises.

Measurements on resonant electric circuits have to be executed discussing enforced oscillations as well as eigen resonance effects.

Experiments with magnetically coupled coils in a so called Helmholtz configuration have to be carried out by the students.

Also some virtual experiments on forces in electrostatic configurations are part of the laboratory. Numerical in-house software packages have to be applied for those experiments.

Finally the braking action of induced eddy currents in a DC electric machine is elaborated in details. Various effects of the set up on the eddy current braking action shall be figured out by the students.

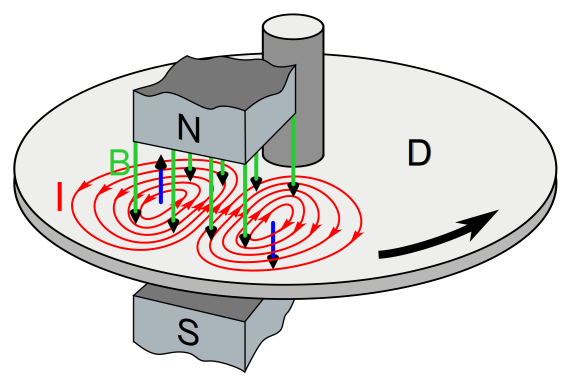
Induced eddy currents in a rotating conductive disk

Theory of Electrical Engineering (437.252/253)

This course extends the description of electromagnetic fields from the course Electrodynamics of a more general description including tensor analysis. A special focus will be drawn to the description and computation of electromagnetic forces (Maxwell’s force tensor, method of virtual work principle) and electromagnetic waves (propagation in infinite homogeneous space, retarded potentials, Hertz dipole, guided waves, transversal magnetic and transversal electric modes, wave guides). Analytic solutions will be obtained by applying the method of fictitious charges, separation of variables, and conformal mapping. For most practical applications, just numerical methods will provide a solution. In doing so, we will discuss the method of finite differences, variational methods (Ritz procedure), and the method of finite elements.

Magnetic flux lines within a T-Joint of a power transformer (left), Eddy current flux lines in a metal sheet above the exciting coil (induction heating) (right)

Computational Electromagnetics (437.121/122)

The course focuses on numerical methods for the solution of electric and magnetic field problems. The Finite Element (FE) formulations for electrostatics, stationary current flow field, static magnetic fields, and quasi-stationary fields (eddy currents) are discussed in detail. In doing so, formulations for the electric scalar potential, electric vector potential, gauged and ungauged magnetic vector potential and electric scalar potential, gauged and ungauged electric vector potential and magnetic scalar potential are derived. In addition, topics towards periodic and antiperiodic boundary conditions, nonlinear and anisotropic material characteristics, and active permeability at time-harmonic problems with nonlinear material behaviour are presented. Practical applications will be grounding systems, high voltage conductors, cables, shielding of electric fields, current flow in melting pots, magnetic fields of high voltage conductors, shielding of magnetic fields, electric power transformers, and dynamic shielding of magnetic fields.

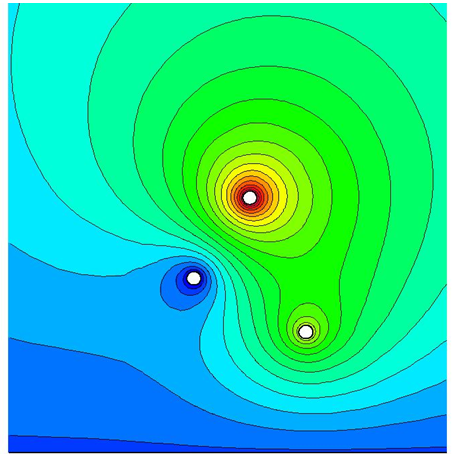
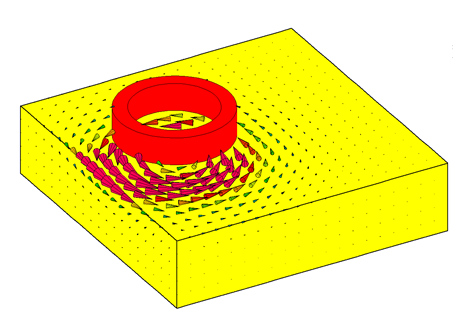
Electric potential of three spheres at different voltages above ground (left), Eddy currents in a copper late (exciting coil above) (right)