Number theory

The research group in number theory exists since 1990. It has grown considerably since then:

Professors

• Robert Tichy (Discrepancy theory, Diophantine equations, analytic and algorithmic number theory, Quasi-Monte Carlo methods and applications in mathematical finance)
• Peter Grabner (Uniform distribution and arithmetic dynamical systems, asymptotic analysis, analytic combinatorics, Fractal Structures in Number Theory)
• Christoph Aistleitner (probabilistic methods in analysis and number theory, analytic number theory, limit laws in probability)
• Christian Elsholtz (combinatorial and additive number theory, analytic number theory, prime numbers, diophantine equations)
• Christopher Frei (analytic number theory and algebraic geometry, lattice points on varieties)

PostDocs

• Daniel El-Baz analytic number theory, homogeneous dynamics, point processes, probabilistic number theory.
• Sebastian Heintze  (Diophantine equations, linear recurrence sequences)
• Dijana Kreso (diophantine equations, polynomials)
• Emily Quesada Herrera (Analytic number theory, Riemann zeta-function, Fourier uncertainty, binary quadratic forms)
• Nick Rome (analytic number theory, Diophantine equations, arithmetic statistics)
• Agamemnon  Zafeiropoulos

PhD students:

• Eren Gökmen, Buket
• Frühwirt, Lorenz
• Führer, Jakob
• Hansen, Willem
• Henry, Michael Andrew
• Maryna Manskova
• Stefanescu, Eduard

Honorary Professors:

Pethö, Attila

Wüstholz, Gisbert.

Former members:

• Soumya Bhattacharya
• Pierre Bienvenu (additive combinatorics, higher order Fourier analysis)
• Bence Borda (discrete and continuous uniform distribution, random walks on groups)
• Kwok Chi Chim (number theory, Baker's method)
• Mahadi Ddamulira
• Ujué Etayo (uniform point distributions on spheres and manifolds, quadrature rules, asymptotic analysis, real complexity theory)
• Benjamin Klahn
• Thomas Lachmann
• Gabriel Lipnik
• Manuel Hauke
• Antoine Marnat (geometric number theory, Diophantine approximation)
• Paolo Minelli
• Stefan Planitzer (analytic number theory, primes, diophantine equations)
• Agamemnon Zafeiropoulos
• Ligia-Loreta Cristea (fractal geometry, topology of fractals, discrete structures, uniform distribution,digital expansions, combinatorics on words)
• Dijana Kreso (diophantine equations, polynomials)
• Kostadinka Lapkova (analytic number theory, class numbers, divisor estimates)
• Marc Munsch (analytic number theory, L-functions, theta functions, modular forms, character sums
• Ivan Rasskin (discrete geometry, fractals in Number Theory, Knot Theory)
• Athanasios Sourmelidis (analytic number theory, L-functions)
• Marc Technau
• Niclas Technau (number theory, analysis, and probability theory)
• Mario Weitzer (arithmetic dynamical systems, discrete geometry)
• Michael Wibmer (algebraic dynamics, difference equations)
• Daodao Yang (analytic number theory)

Former members of the group also include: Clemens Fuchs (Salzburg), Clemens Heuberger (Klagenfurt), Manfred Madritsch (Nancy), Bruno Martin (Calais) Thomas Stoll (Nancy), Martin Widmer (Royal Holloway, London).

We have regular contacts with colleagues in Debrecen, Zagreb, Budapest, Royal Holloway, Marseille, Nancy, Paris, Beersheba, Rostock, UNSW and Macquarie University, and many other places.

Our seminars are announced in the general TU Graz maths seminar list (fosp).

There are further seminars in algebra and number theory at Karl Franzens University Graz.

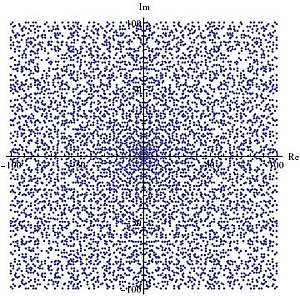
The picture on the left hand side shows the Gaussian primes around the origin, with real and imaginary part in [-100,100]. While these primes appear to be quite dense it is an open problem if it is possible to walk from the origin to infinity with steps of size bounded by an absolute constant. (The problem was posed at the International congress of mathematicians in 1962 by Basil Gordon.)

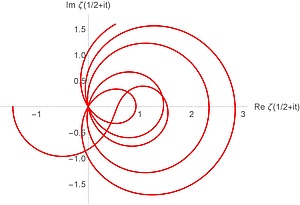
The picture on the right hand side shows the real and imaginary part of the Riemann zeta function zeta(1/2+it) in the complex plane, for t in the range from 0 to 34.